ACKNOWLEDGEMENTS
I wish to express my deep gratitude to the U. S. Geological Survey, the National Oceanic and Atmospheric Administration, and the magnetic observatories at Kakioka, Hermanus and Alibag for their cooperation in providing the valuable data. I am greatly indebted to R. S. Kennon and D. P. Poros for their valuable contributions in deriving the Dst index and in producing the tables and figures presented in this volume, and to Ms. Shirley Cain for her participation in the development of the computer programs in the early phase of this project. I wish to thank Drs D. Van Sabben and J. A. As, and more recently Drs A. Berthelier and M. Menvielle, for their support and assistance in publishing this volume.
Masahisa Sugiura
Note added in June 1991
The publication of this volume was originally planned, and materials were prepared, in the 1970's. However, the publication was delayed in connection with the cessation of activity of the ISGI office at De Bilt, The Netherlands, and it was resumed after the transfer of the ISGI Publication Office to Saint-Maur-des-Fossés, France.
This volume is based on the manuscript updated in 1981, except that the plots and tables have been further updated to 1986.
Present Addresses:
Masahisa SUGIURA
Institute of Research and Development
Tokai University, 2-28 Tomigaya, Shibuya-ku
Tokyo 151, Japan
Toyohisa KAMEI
Data Analysis Center for Geomagnetism and
Space Magnetism Faculty of Science, Kyoto University
Kyoto 606, Japan
FOREWORD
A starting point for the studies concerning Dst derivation can be found at the end of the forties, when J. Bartels, chairman of the Committee on Characterization of Magnetic Disturbances of IATME and IAGA, stimulated studies for deriving an index monitoring the equatorial ring current variations.
Preliminary attempts for defining such an index were made at the end of the fifties and the beginning of the sixties (Kertz, 1958, 1964; Sugiura, 1964). Then Sugiura and Hendricks (1967) proposed a derivation scheme. An improved version developed by Sugiura and coworkers was adopted by IAGA (Resolution 2, p. 123, in IAGA Bulletin 27, Madrid, 1969).
However, due to modifications in the station network, and to improvements added later to the derivation process, the sets of Dst indices published so far are slightly different:
·
Hourly values of Dst for the years 1957-1970, based on the data of three stations, have been published by M. Sugiura and D. J. Poros in the report X-645-71-278 of the Coddard Space Flight Center, a report which supersede earlier Dst publications by Sugiura and co-workers.·
Hourly Dst values for the IGY (1957-1958), based on the-data of eight stations, are given in the Annals of the IGY (vol. 35). The same volume contains three-hourly values of Dst for the IGY as determined by Kertz in a somewhat different way.·
Hourly Dst values are also yearly published in the IAGA-Bulletin N°32 series from 1970 onwards. More recently, M. Sugiura recomputed an homogeneous series of Dst values, using the data of four stations. Therefore the International Service of Geomagnetic Indices publishes in this reference IACA Bulletin the equatorial Dst index values for the thirty years 1957-1986, together with a description of the used derivation scheme. Further details about meaning and use of Dst indices can be found in Mayaud (1980) and in Rangarajan (1990).Let us emphasize that, according to the authors, the Dst data given in this volume supersede all other earlier versions.
We gratefully acknowledge Dr M. Sugiura for his kind cooperation in the course of preparation of the final version of this Bulletin.
Annick Berthelier, Michel Menvielle
Saint-Maur, Juin 1991.
1. INTRODUCTION
It has long been known that the horizontal component, H, of the geomagnetic field is depressed during periods of great magnetic disturbances and that the recovery to its average level is gradual (Broun, 1861; Adams, 1892; Moos, 1910). Comprehensive analyses of magnetic storm morphology have been made by Chapman (1935, 1952 and earlier papers referred to therein), Vestine et al. (1947), Sugiura and Chapman (1960), and many others (see Akasofu and Chapman, 1972).
These studies have shown that at equatorial and mid latitudes the decrease in H during a magnetic storm can approximately be represented by a uniform magnetic field parallel to the geomagnetic dipole axis and directed toward south. The magnitude of this axially symmetric disturbance field varies with storm-time, defined as the time measured from the storm onset. The onset of a magnetic storm is often characterized by a global sudden increase in H, which is referred to as the storm sudden commencement and denoted by ssc. The list of storm sudden commencement is established by the Observatori del'Ebre. It is published in the ISGI Monthly Bulletins (preliminary list) and the IAGA Bulletin N°32 series; the latter series also lists the time of the ssc's. These storm sudden commencements are indicated by triangles in the Kp musical diagrams established by the Institut für Geophysik der Universitat Göttingen, and published in the IAGA-Bulletin N°32 series.
Following the ssc, the H component typically remains above its average level for a few hours; this phase is called the initial phase of the storm. Then a large global decrease in H begins, indicating the development of the main phase of the storm. The magnitude of the decrease in H represents the severity of disturbance. Although the above description gives statistical average features of magnetic storms, the variations in individual cases differ greatly from one storm to another.
We denote by Dst the disturbance field, which is axially symmetric with respect to the dipole axis, and which is regarded as a function of storm-time. If an index monitoring the Dst in H is derived continuously as a function of UT, this variation will clearly indicate the occurrences of magnetic storms and their severity when they occur. Furthermore, even in the absence of distinct magnetic storms, this index will continuously monitor disturbances that are smaller in magnitude than those usually called magnetic storms, or disturbances that begin gradually without a well-defined commencement. Thus, the Dst variation so derived will provide a quantitative measure of geomagnetic disturbance that can be correlated with other solar and geophysical parameters. It is for these purposes that the Dst index is derived and published through the IAGA on a continuous basis.
2. METHOD OF DERIVATION OF THE Dst INDEX
2.1. The network
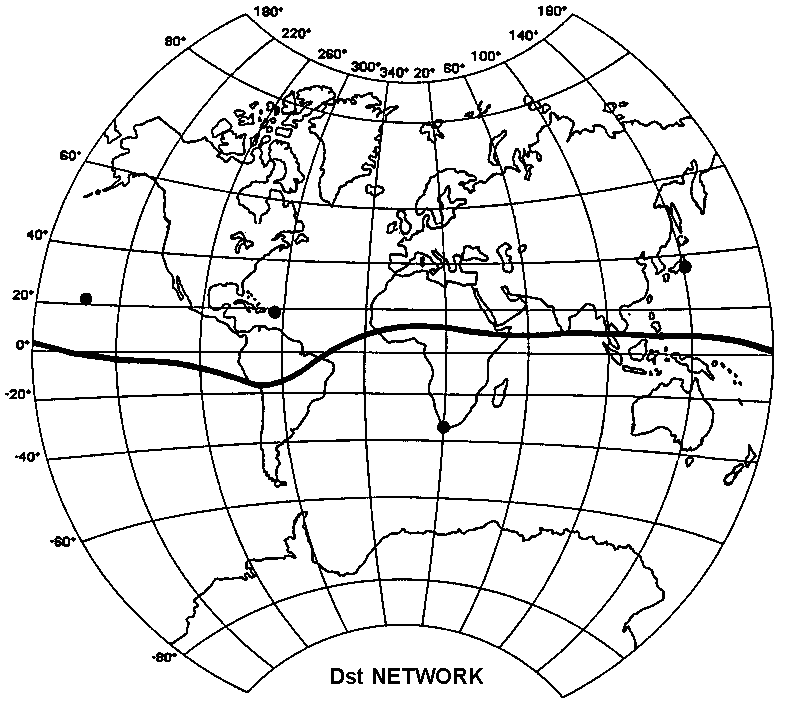
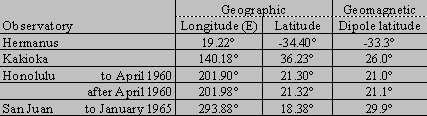
For the derivation of the Dst index presented in this report, four magnetic observatories, Hermanus, Kakioka, Honolulu, and San Juan are used. These observatories were chosen on the basis of the quality of observation and for the reason that their locations are sufficiently distant from the auroral and equatorial electrojets and that they are distributed in longitude as evenly as possible. The coordinates of the observatories are given in
Table 1, and a map of the network is given in Figure 1.
Figure 1 – The Dst Network

Table 1 – Coordinates of the Observatories
2.2 Derivation process
2.2.1. Baseline
The baseline for H is defined for each observatory in a manner that takes into account the secular variation. For each observatory, the annual mean values of H, calculated from the "five quietest day" for each month, form the database for the baseline. It should be remembered that the final Dst values are determined after each calendar year and that therefore in this determination the annual mean values are available only up to and including the year (referred to below as the current year) for which the Dst is to be deduced. The baseline is expressed by a power series in time and the coefficients for terms up to the quadratic are determined by the method of least squares, using the annual means for the current year and the four preceding years. Thus, the baseline, H base is expressed as
![]() (1)
(1)
Where ![]() is time in years measured from a reference epoch.
is time in years measured from a reference epoch.
It is noted here that if the polynomial expansion of the annual means is made in a straightforward manner as described above, an artificial discontinuity, although seldom large enough to be recognized by a casual inspection, can be introduced between the baseline value for the last hour of one year and that for the first hour of the following year, because these two baseline values are calculated from two different polynomials. To minimize such a discontinuity the polynomial determination is actually made in two steps. From the polynomial expansion determined in the first step, the baseline value at the end of current year is calculated. In the second step, this value is included as an additional data point in the polynomial fitting. This procedure has been found to be satisfactory.
The baseline value H base(T) calculated from (1) for each UT hour of the current year is subtracted from the observed H value. H obs(T) :
![]() (2)
(2)
The deviations, ![]() H(T), form the data base in the following derivation for each of the observatories.
H(T), form the data base in the following derivation for each of the observatories.
2.2.2. Sq elimination
The solar quiet daily variation, Sq, is derived for each observatory as follows. The average Sq variation for each month is determined from the values of H(T) for the internationally selected five quietest days of the month. These quietest days are determined in UT. In order to define an average Sq variation for the local day of each observatory, we form the averages for the local hours using five local days that have the maximum overlap with the international five quietest days. Also, using hourly values immediately before and immediately after the local days selected, we evaluate the linear change and subtract it from the Sq variation. In this manner we remove from Sq the non-cyclic change, which is part of Dst variation, and also evaluate Sq from the midnight level.
The 12 sets of the monthly average Sq so determined for the year are expanded in a double Fourier series with local time, t, and month number, s, as two variables:
![]() (3)
(3)
This representation allows us to calculate Sq(T) at any UT hour, T, of the year. This procedure is applied to each observatory.
2.2.3. Hourly Equatorial Dst Index
For each observatory the disturbance variation, D(T), is defined by :
![]() (4)
(4)
Then D(T) is averaged over the four observatories and normalized to the dipole equator by :
![]() (5)
(5)
where the denominator is the average of the cosines of the dipole latitudes, ![]() (
(![]() = 1,4), of the observatories contributing to the average. This normalization procedure has been found to minimize undesired effects from missing hourly values.
= 1,4), of the observatories contributing to the average. This normalization procedure has been found to minimize undesired effects from missing hourly values.
2.3. Remarks on the Dst Derivation
The above procedure, including the production of tables and plots, is automated to the maximum extent possible. However, techniques have been devised to detect errors at various stages. By this method, numerous errors have been detected in the observatory data and subsequently corrected. The method of the derivation of Dst has been improved over the years; for an earlier version, see Sugiura (1964). It may appear that the method could be improved further. For instance, it might be thought that the selection of the quiet days to be used for the average Sq can be improved. However, any selection of quiet days would introduce arbitrariness. Also, Sq is a dynamic variation which often changes over time periods of a few hours to several days, and therefore, the modeling of Sq has a statistical meaning only. Thus we chose to use the internationally selected five quietest days of each month. A statistical study can readily be made on these quiet days and if necessary, corrections can be applied to the Dst index for any modifications on Sq.
Obtaining Dst on a routine basis with a higher time-resolution than I hour would not be feasible unless all the magnetometers at the Dst observatories are converted to digital systems. Even if the magnetometers are made digital, it is likely that high time-resolution Dst data would be worthwhile to derive only for specific periods or events.
2.4. Reference level for the Dst index
The reference level for Dst is set so that on the internationally designated five quietest days the Dst index is zero on the average. However, even on these quiet days there exists a southward directed magnetic field produced by the equatorial current system in the magnetosphere, which is often referred to as the quiet time ring current. The magnetic field depression in the magnetosphere has been extensively surveyed by the OGO 3 and 5 satellites (e.g. Sugiura and Poros, 1973). According to the OGO 5 observations, the magnetic field depression near the dipole equator at geocentric distances of 2.3 to 3.6 earth-radii is statistically about 45 nT when Dst is zero (Sugiura, 1973). The magnitude of this field depression is likely to decrease toward the Earth, but there are no definitive observations to date to provide the distribution of the magnetic field at geocentric distances less than 2 earth radii. A preliminary study with Magsat data taken at 350 to 560 km altitudes shows that at the surface of the Earth the axially symmetric external field is estimated to be -25 nT when Dst is zero (Langel et al., 1980). Although this value seems reasonable, the absolute reference level for the Dst variation remains to be studied in the future. For instance, the off-set of Dst may vary with solar cycle.
3. INTERPRETATION OF THE Dst INDEX
The Dst index represents the axially symmetric disturbance magnetic field at the dipole equator on the Earth's surface. Major disturbances in Dst are negative, namely decreases in the geomagnetic field. These field decreases are produced mainly by the equatorial current system in the magnetosphere, usually referred to as the ring current. The neutral sheet current flowing across the magnetospheric tail makes a small contribution to the field decreases near the Earth. Positive variations in Dst are mostly caused by the compression of the magnetosphere from solar wind pressure increases.
It is known that the disturbance field is generally not axially symmetric. In particular, in the developing phase of a magnetic storm the asymmetric disturbance field can be even greater than the symmetric part (e.g. Sugiura and Chapman, 1960; Akasofu and Chapman, 1964). In the asymmetric disturbance field, the field decrease is usually largest in the dusk sector. To monitor the asymmetric disturbance field we expand for each UT hour, T, the disturbance field D(T) in a Fourier series in local time and determine the amplitude and phase of the diurnal component. During the Magsat operation, Dst and diurnal and semi-diurnal components of D were derived and made available on the Magsat data tape (Langel et al., 1981). For this period, the data from the four Dst observatories were supplemented by those from Alibag to improve the longitudinal coverage. The asymmetric disturbance field has usually been attributed to a partial ring current (Akasofu and Chapman, 1964; Cahill, 1966; Frank, 1970; Fukushima and Kamide, 1974). However, it has also been suggested that the asymmetric disturbance field may be produced by a net Birkeland current flowing into the ionosphere near noon and flowing out near midnight (Crooker and Siscoe, 1981). The source for asymmetric disturbance field therefore remains to be resolved in the future.
For many years it was tacitly assumed that the ring current is carried by hydrogen ions. However, recent satellite observation have shown that oxygen and helium ions form significant components of the ring current particles in the energy range below 17 Kev, suggesting that the ionosphere is a major source of the storm time ring current (Shelley, 1979). Satellite observations of the decay of the ring current also seem to indicate the presence of oxygen and helium (Smith et al., 1881). The ring current ions with energy greater than 600 Kev have a composition suggestive of solar wind origin (Williams, 1980). However, the composition of the ions forming the bulk of the ring current energy density, i.e. ions with energies approximately between 20 and 600 Kev, has not been directly measured (Williams, 1981). For the formation of the storm time ring current, such processes as the earthward convection of the tail plasma sheet and adiabatic inward motion of the outer zone radiation belt ions both due to enhanced dawn-dusk electric fields, acceleration of ionospheric ions by electric fields, and in-situ acceleration of the plasma at the plasmasphere-plasma sheet interface appear to be involved.
4. PRESENTATION OF THE BULLETIN
This IAGA Bulletin N°40 presents the values of the equatorial Dst index for the years 1957 to 1986.
The plots of the hourly Dst values are given in the following Section 2 (pages 15 - 46). In the figures, the solar rotation numbers are indicated on the right, and the day numbers, 1 to 27, in each solar rotation are shown at the bottom.
Annual tabulations of the daily, monthly and annual averages of the equatorial Dst index are given in Section 3 (pages 47 - 63).
The monthly tabulations of the hourly values of the equatorial Dst index are given in Section 4 (pages 65 - 246). In the monthly tables, 24 hourly average Dst values are given for each day for the 24 hourly UT intervals beginning with 00:00. For instance, the Dst values in the first column (UT = 1) are averages for the UT interval 00:00 to 01:00.
The Dst data given in this volume supersede all other earlier versions.
5. DATA AVAILABILITY
The hourly values from 1957 onwards are available on magnetic tape and on CD Rom at the World Data Center-A, and on floppy disk at the PC standard at the ISGI Publication Office (see addresses below).
WDC-A World Data Center-A for Solar-Terrestrial Physics
NOAA code E/GC2, 325 Broadway
BOULDER, Colorado 80303, U.S.A.
Telephone 1 303 497 6324
Telex 592 811 NOAA MASC BDR
Telefax 1 303 497 6513
ISGI International Service of Geomagnetic Indices
Service International des Indices Géomagnétiques
CRPE -CNRS, 4, Avenue de Neptune
F-94107 SAINT MAUR DES FOSSES CEDEX, France
Telephone 33 1 48 86 12 63
Telex 264 498 OBSMAUR
Telefax 33 1 48 89 44 33
6. REFERENCES
Adams, W.G., Comparison of simultaneous magnetic disturbance at several observatories, Phil. Trans. London (A), 183, 131, 1892.
Akasofu, S.-I. and S. Chapman, On the asymmetric development of magnetic storm field in low and middle latitudes, Planet. Space Sci., 12, 607, 1964.
Akasofu, S.-I. and S. Chapman, Solar Terrestrial Physics, Oxford University Press, Oxford, 1972.
Broun, J.A., On the horizontal force of the Earth's magnetism, Proc. Roy. Soc. Edinburgh, 22, 511, 1861.
Cahill, L.J., Jr, Inflation of the inner magnetosphere during a magnetic storm, J. Geophys. Res., 71, 4505, 1966.
Chapman, S., The electric current-systems of magnetic storms, Terr. Mag. Atomos. Phys., 40, 349, 1935.
Chapman, S., The morphology of magnetic storms: an extension of the analysis of Ds, the disturbance local-time inequality, Annali di Geofisica, 5, 481, 1952.
Crooker, N.U., and G.L. Siscoe, Birkeland currents as the cause of the low-latitude asymmetric disturbance field, J. Geophys. Res., 86, 11201, 1981.
Frank, L. A., Direct detection of asymmetric increases of extraterrestrial ring proton intensities in the outer radiation zone, J. Geophys. Res., 75, 1263, 1970.
Fukushima, N., and Y. Kamide, Partial ring current models for world geomagnetic disturbances, Rev. Geophys. Space Phys., 11, 795, 1973.
Langel, R.A., R.H. Estes, G.D. Mead, E.B. Fabiano, and E.R. Lancaster, Initial geomagnetic field model from Magsat vector data, Geophys. Res. Letters, 7, 793, 1980.
Langel, R.A., J. Berbert, T. Jennings, and R. Horner, Magsat data processing: a report for investigators, NASA Technical Memorandum 82160, Goddard Space Flight Center, 1981.
Moos, N.A.F., Magnetic observations made at the government observatory, Bombay, for the period 1846 to 1905, and their discussion, Part II: the phenomenon and its discussion, Bombay, 1910.
Shelley, E.O., Heavy ions in the magnetosphere, Space Sci. Rev., 23, 465, 1979.
Smith, P.H., N.K. Bewtra, and R.A. Hoffman, Inference of the ring current ion composition by means of charge exchange decay, J. Geophys. Res., 86, 3470, 1981.
Sugiura, M., Hourly values of equatorial Dst for the IGY, Ann. Int. Geophys. Year, 35, 9, Pergamon Press, Oxford, 1964.
Sugiura, M., Quiet time magnetospheric field depression at 2.3-3.6 Re, J. Geophys. Res., 78, 3182, 1973.
Sugiura, M., and S. Chapman, The average morphology of geomagnetic storms with sudden commencement, Abandl. Akad. Wiss. Göttingen Math. Phys. Kl., Sondernheft Nr.4, Göttingen, 1960.
Sugiura, M., and D.J. Poros, A magnetospheric field model incorporating the OGO-3 and-5 magnetic field observations, Planet. Space Sci., 21, 1763, 1973.
Vestine, E.H., L. Laporte, I. Lange, and W.E. Scott, The geomagnetic field, its description and analysis, Carnegie Institution of Washington Publication 580, Washington D.C., 1947.
Williams, D.J., Ring current composition and sources, in Dynamics of the magnetosphere, ed. S.-I. Akasofu, D. Reidel Publishing Company, p.407, 1980.
Williams, D.J., Ring current composition and sources: an update, Planet. Space Sci., 29, 1195, 1981.
Additional References (quoted in the Foreword)
Kertz, W., Ein neues Mass für die Feldstärke des erdmagnetischen aquatorialen Ringstroms, Abh. Akad. Wiss. Göttingen Math. Phys., 2, 83pp, 1958.
Kertz, W., Ring current variations during the IGY, Ann. Int. Geophys. Year, 35, 49, 1964.
Mayaud, P.N., Derivation, Meaning, and Use of Geomagnetic Indices, Geophysical Monograph 22, American Geophysical Union, Washington D.C., 1980.
Rangarajan, G.K., Indices of geomagnetic activity, in Geomagnetism, p.323, ed. by J.A. Jacobs, Academic Press, London, 1989.
Sugiura, M., and S. Hendricks, Probisional hourly values of equatorial Dst for 1961, 1962 and 1963, NASA Tech. note D-4047, 1967.