(23) Frames of Reference: The Centrifugal ForceThe other case of a moving frame of reference studied here is:
(2) The local frame rotates around some fixed point. An earlier section described motion in a circle and introduced the centripetal force which makes such motion possible. That is a force towards the center of rotation, of magnitude
To anyone who has not studied motions and accelerations, "centripetal" is probably a new word. However, most people are aware of the outwards-pushing centrifugal force, the force which flings you away from the center of rotation in a car speeding around a corner. In a popular carnival ride, that is the force which pushes you against a rotating drum, holding you in place even when you are upside down. What is the connection? As will be seen, the centrifugal force is not a "real" force, in the sense that in any motion calculated "in the frame of the universe" (or in one moving uniformly with respect to the universe) it does not appear at all. In such a frame, if an object moves around a circle, a centripetal force is needed to maintain that motion--or else it flies off at a tangent, with constant velocity along a straight line. Unfortunately, if you sit (for instance) in a roller coaster car going around a vertical loop (as in the picture above, from an amusement park in Japan), it is a bit difficult to visualize your motion with respect to the fixed Earth. (To demonstrate that difficulty, we later solve the motion from that viewpoint.) It is much simpler to orient yourself with respect to the car in which you sit.
EquilibriumEquilibrium is the state at which all forces balance each other, so that no net motion exists. Under usual conditions, this happens when all forces on the object in equilibrium add up to zero:
(If the above condition does not hold, the object will move inside the rotating frame and the situation is more complicated. For now let it just be said that yet another force then enters the equations, the Coriolis force, discussed qualitatively in the next section.)
That result was alread derived from circular motions two sections back. The difference between the equations governing such motions in the outside frame
ExamplesWhen calculating the motions of the oceans and the atmosphere, it is much easier to use reference points on the rotating Earth and add a centrifugal force to all equations. That is one reason why the observed acceleration g due to gravity departs from the average value of 9.81: at the equator, the centrifugal force must be subtracted from the force of gravity, while at the pole no centrifugal force exists. Observations of g give values from 9.78 at the equators to 9.83 at the poles, but the centrifugal force is responsible for only part of that difference. The rest arises because the Earth is not a perfect sphere: the centrifugal force of its rotation causes its equator to bulge out, making the surface there more distant from the Earth´s center and thus weakening the gravitational pull.
If you try to solve this problem from the point of view of the outside world, the situation can be confusing. At point A, on the top of the loop, both gravity and the centripetal force point downwards. So what is there that can keep riders in their seats? Let us try solve that motion, using the concept of the centripetal force. A car going around a loop, with radius R and velocity V, is accelerating at a rate of V 2/R towards the center (as long as it stays on the rails), and is therefore subject to a centripetal force mV 2/R, also directed to the center. When the car is at point A, that force points downwards. Let "down" be now be taken as the positive direction along the vertical axis. The centripetal force is provided by two sources: the weight mg of the car, directed downwards, and the reaction FR of the rails. We have at point A
We thus require FR > 0, that is
continue along a straight line to point B, in accordance with Newton's first law. --If only gravity acted, it would follow a parabola to point C. --For the rails to exert a positive pressure, they must constrain the car to a tighter curvature than gravity alone, forcing it to move to point D. |
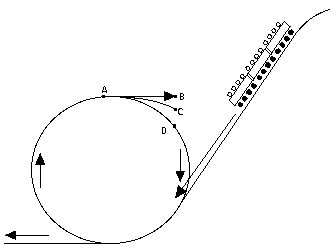 Another example is the "loop the loop" feature found on some roller coasters in amusement parks. There the track descends on a long slope and then, at the bottom, turns in a complete circle (drawing) before leveling out again. At the point marked "A" the riders are briefly turned upside down, but no one ever falls out. How come? And how high must the starting point S be above A to ensure it?
Another example is the "loop the loop" feature found on some roller coasters in amusement parks. There the track descends on a long slope and then, at the bottom, turns in a complete circle (drawing) before leveling out again. At the point marked "A" the riders are briefly turned upside down, but no one ever falls out. How come? And how high must the starting point S be above A to ensure it?

