(8c) The Moon's Distance--2Hipparchus (and possibly Aristarchus before him) also derived the Moon's distance from the duration of a lunar eclipse. Because the Earth casts a much larger shadow than the Moon, such an eclipse usually darkens the entire Moon, for several hours. Let t be the length of the eclipse, from the moment the shadow touches the middle of the Moon to the moment it again uncovers it. If the Sun is assumed to be very distant, and if the Moon crosses the middle of the shadow (if not, corrections must be made), the width of the shadow is expected to be about 2r, twice the Earth's radius r. Let T be the period of the Moon's motion, in a frame rotating with the Earth around the Sun (new Moon to new Moon). Then if R is the Moon's distance, the path covered by the Moon in that period (in the rotating frame) is (2pR) where p = 3.1415926.... It follows that
and that gives the ratio R/ r, the Moon's distance expressed in Earth radii.
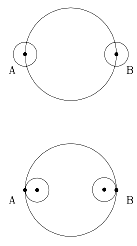
Actually, a correction is needed before that equation can be applied. If the Sun were point-like, very small, then a point on the Moon would enter the shadow when point A on Earth covered the center of the Sun, and would end when point B uncovered it (top drawing). |