(8a) Distance to the Horizon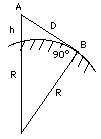
Imagine you were standing at an elevation of h meters above the ocean and looking out across the water. What is the distance D to the horizon? It can be calculated, if you know the radius R of the Earth.
Your line of sight to the horizon is a tangent to the Earth--a line which touches the sphere of the Earth at just one point, marked B in the drawing here. If O is the center of the sphere of the Earth, by a well-known theorem of geometry such a tangent is perpendicular to the radius OB, that is, it makes a 90o angle with it. It follows that the triangle OAB obeys the theorem of Pythagoras, which here can be written (OA)2 = (AB)2 + (OB)2 or if the length of each line is spelled out (R + h)2 = D2 + R2 By an algebraic identity (derived in the "mathematical refresher"), the left-hand side equals R2 + 2Rh + h2, giving R2 + 2Rh + h2 = D2 + R2 If now R2 is subtracted from both sides and the remaining terms on the left are rearranged h(2R + h) = D2 The diameter 2R of the Earth is much bigger than h, and therefore the error introduced if (2R+h) is replaced by 2R is very, very small. Carrying out this replacement gives 2Rh = D2 where SQRT stands here for "square root of". This equation lets one calculate D--in kilometers, if h and R are given in kilometers--but one it is also possible to simplify further: SQRT(2Rh) = (SQRT(2R))(SQRT(h)) with the two square roots multiplied. Using R = 6371 km, SQRT(2R) = 112.88, giving D = 112.88 km SQRT(h) If you are standing atop a mountain 1 km high, h = 1 km and your horizon should be 112.88 km away (we neglect the refraction of light in the atmosphere, which may modify this value). From the top of Mauna Kea on Hawaii, an extinct volcano about 4 km high (also the site of important astronomical observatories), the horizon should be about twice as distant, 226 km. On the other hand, standing on the beach with your eyes 2 meters = 0.002 km above the water, since SQRT(0.002) = 0.04472, the horizon is only 5 km distant. 
The calculation should also hold the other way around. From a boat on the ocean you should begin seeing the top of Mauna Kea after you pass a distance of 226 km (again, not accounting for refraction). On November 15, 1806, Lieutenant Zebulon Pike of the US Army, leading an exploration party across the plains of the midwestern US, saw through his spyglass the top of a distant peak, just above the horizon. It took his party a week to cover the 100 miles to the mountain, which is now known as Pike's Peak, one of the tallest in Colorado. Pike actually tried to climb to its top, but the snow and the unexpected height of the mountain forced him back. |
