(17) Mass
Newton solved the riddle by proposing that the greater amount of substance in the iron ball had two different effects: it increased the downward pull on the ball, but also increased its resistance to motion--any motion. The increase in one was matched by an increase in the other, resulting in the heavy ball falling no faster. According to Newton, every object had two independent properties:
Newton was the first to realize that when we say that (for instance) a bowling ball is "heavy", two different things are implied:
The first kind of heaviness is associated with gravity and is quite familiar. The second is most clearly seen when the ball moves horizontally, a motion on which gravity has a much smaller effect. When our arm accelerates the ball before sending it down the bowling alley, we find it much harder to give the same speed to a heavy ball than to a light one. Similarly, it is much harder to start a heavily loaded wagon rolling than it is to do so with an empty one. It may be argued that, of course the loaded wagon is harder to move--because it presses down on the ground with a greater weight, creating a greater friction that opposes the motion. Quite true: however, it is also harder to stop the rolling wagon when it is loaded, even though friction now helps our effort. It is the fact that the loaded wagon has a greater mass that gives it a larger inertia, a larger tendency to oppose any change in its state of rest or of constant motion in a straight line. Measuring Mass on a Space StationIn 1973 NASA put in orbit the space station Skylab, and its experiments included a careful monitoring of the health of the crew. One important quantity was the body mass of the astronauts. Here on Earth it would be called "body weight" and would be measured by weighing a person on scales. However, scales would not work on a space station. They use gravity, balancing its force on the astronaut's body against a calibrated spring or against the force of gravity on some calibrated weights. It is not correct to say that gravity does not exist on an orbiting spacecraft (if it did, the spacecraft would fly away, never to return). Rather, in the "zero g" environment of the space station, gravity is already doing all it can in moving the station in its orbit, and none of it is evident inside the station. Since the orbit is curved, the first law is not violated by requiring a force to maintain it. How can mass be measured there? One gets a clue from clocks, all of which need some sort of device that gauges the passage of time. "Grandfather clocks" use a pendulum, whose back-and-forth motion always requires a fixed amount of time, depending on its length. Pendulum motion depends on gravity and would obviously not work in a mechanical wristwatch, which might be placed in different positions. It is also unsuitable for timekeeping aboard a rolling and pitching ship, which used to be essential for accurate navigation before satellites took over the job. The clocks originally developed for such uses (see the book "Longitude" by Dava Sobel) depended instead on a balance wheel, turning periodically back and forth--clockwise, then counter-clockwise, then clockwise again--against a spiral spring. Gravity was not involved. Modern electronic watches replace the wheel with a vibrating quartz crystal, acting somewhat like a tuning fork: the motion is much faster, but transistor circuits can easily count the vibrations, which are very stable.
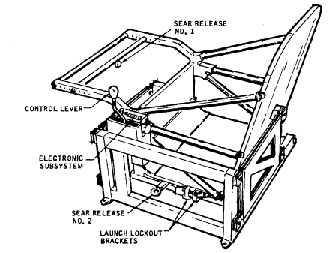
It makes no sense to whirl an astronaut back and forth like a balance wheel to determine body mass. Not only would the ride be unpleasant, but deducing the mass from such observations is almost impossible, since each part of the body moves at a different speed, depending on its distance from the axis of rotation. What does work is back-and-forth oscillation between two springs. Since the oscillation is opposed by inertia, the greater the mass, the slower is the process, and by measuring the frequency of oscillation, a fair idea of body mass can be obtained. A device of this sort was used aboard Skylab, where astronauts sat in a spring-mounted chair which oscillated back and forth. For further details on that experiment, see the next section. |
 Galileo showed convincingly that heavy objects fell no faster that light ones. However, no one could explain why. If an iron ball was pulled down with a much greater force than a wooden one of the same size, why didn't it fall any faster?
Galileo showed convincingly that heavy objects fell no faster that light ones. However, no one could explain why. If an iron ball was pulled down with a much greater force than a wooden one of the same size, why didn't it fall any faster?