|
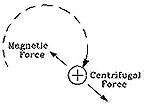
If the string is pulled up while the pendulum is swinging, two things happen. The period T of each swing gets shorter, as noted before. But in addition, the energy E of the pendulum increases, which means the height of each swing becomes larger. For as the pendulum swings, it generates a centrifugal force, and the pull on the string, besides lifting the weight to a higher average position, also has to overcome the resistance of the centrifugal force. That requires an extra input of energy from the force pulling the string, and since energy has to go somewhere, it makes the swing of the pendulum more vigorous.
Incidentally, this process is related to the way children "pump" a swing to make it go higher. The child moves arms, legs and body in a way that works against the centrifugal force, and the energy invested in overcoming this force ends up producing a more energetic swinging motion.(This is a highly simplified explanation and assumes that from the point of view of the child in the swing, nature behaves exactly the same as anywhere else, only a centrifugal force is added. The actual situation can be more complicated.)
It turns out that the product T x E, the period T times the energy E, is
almost a constant. It is not an exact constant, like total energy in a system, but if the rate of change is slow enough, e.g. if the string is pulled rather slowly, it comes very close.
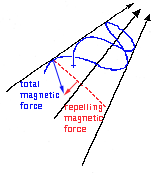
The motion of electrons and ions spiraling around magnetic field lines is also periodic. While the period of a pendulum changes when its string gets longer or shorter, that of a spiraling ion or electron changes as it moves into regions where the magnetic field is weaker or stronger. Just as for a pendulum the product T x E stays very nearly constant, so here too, a certain quality, an "adiabatic invariant," is almost kept at a constant value. From that constancy it is possible to deduce the "mirroring" of particle and many other properties of their motion.
|

 Official GSFC Home Page
Official GSFC Home Page  NASA WWW Home Page
NASA WWW Home Page