Waves in cold plasma

SpaceWeb@SkyNet.oulu.fi - last update: 28 May 1995, 0800 UT

As discussed in context of plasma theories, the thermal kinetic energy of plasma particles is ignored in cold plasmas. In practice this means neglection of the pressure terms in the equations. In the theory of waves, this approximation is justified if the particle thermal velocity is small when compared with the wave phase velocity. Accordingly, for waves with very small phase velocities, warm plasma theory must be used.

Another often used approximation is to consider only electron motion. The theory of wave propagation in a cold homogenous electron gas immersed in a magnetic field (B) is known as magnetoionic theory. The neglection of ions is valid only for high frequency waves, i.e., for frequencies large compared to the ion cyclotron frequency. To go on to the next level of approximation, the theory of high-frequency small-amplitude plane waves propagating in an arbitrary direction with respect to B is called the Appleton-Hartree theory. This was first developed to study wave propagation in the Earth's ionosphere. The restriction of small-amplitude waves makes it possible to use linear perturbation theory, where the wave related variations in the plasma parameters are small when compared to the undisturbed parameters. The use of plane waves makes the equations easier, but implyes no loss of generality, since any wave motion can always be synthesized in terms of plane waves. The hydromagnetic extension of magnetoionic theory deals with multicomponent cold plasma.

In the cold electron gas, important variables are the electron number density and the average electron velocity. They must satisfy

the continuity equation,
the Langevin equation of motion, and
Maxwell's equations

The wave modes are found from the dispersion relation calculated using the above equations. We start investigating the results from a non-magnetized (isotropic) plasma, before including the external magnetic field so important for space physics. Ion motion is not included (but some remarks about ion effects are given).

Non-magnetized cold plasma

There are one oscillation mode and one real wave mode in cold isotropic electron plasma:

electron plasma oscillations
- longitudinal oscillations at electron plasma frequency w(pe)
- electrostatic and stationary (no wave propagation, but note: warm plasma theory reveals the electron plasma waves related to this oscillation)
- inclusion of ions in the cold wave theory changes slightly the oscillation frequency: w=sqrt(w(pe)^2+w(pi)^2) (we talk simply about longitudinal plasma oscillations)
transverse waves
- propagating above the electron plasma frequency, w(pe) (reflection point for the waves)
- note that, for very high frequencies, both phase and group velocities are equal to light velocity c, and we have electromagnetic wave in free space: even the electrons are unable to respond to the rapidly oscillating electric field!
- also here the inclusion of ions into the theory changes the reflection point frequency as above

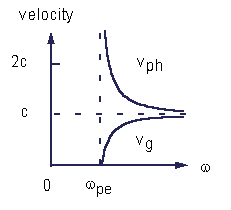
Frequency dependence of the phase and group velocities for the transverse waves in a collisionless isotropic cold electron plasma.

Magnetized cold plasma

Things get quite a bit more complicated when external magnetic field B is taken into account (even with the Appleton-Hartree approximation):

Propagation parallel to B (three wave modes)

longitudinal electron plasma oscillations (as for isotropic plasma)
transverse right-hand circularly polarized waves, RCP
- the transverse electric field of the wave rotates in the same direction as the electrons about the B field
- at electron gyrofrequency, a resonance is created, and energy is transformed from the wave to the electrons
- plasma electrons can be heated with this method
- waves propagate in two frequency ranges: w<w(ce) and w>w(02)
- RCP waves at lower frequencies than the electron gyrofrequency w(ce) are commonly known as electron cyclotron waves
- at very low frequency region (but well above the w(ci)) whistler waves are found
transverse left-hand circularly polarized waves, LCP
- if ion motion is not taken into account, LCP waves propagate only when w>w(01)
- if ion motion is taken into account, w<w(ci) branch is created
  1. resonance is created with ions
  2. ion cyclotron waves are found

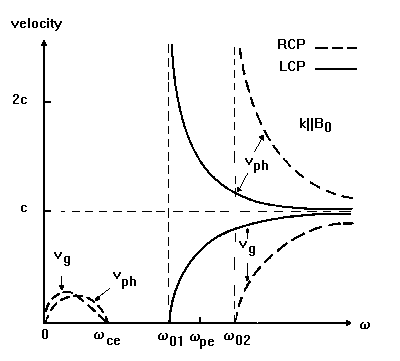
Frequency dependence of the phase and group velocities for the transverse RCP and LCP waves propagating along magnetostatic field in a collisionless cold electron plasma.

An important point is that, in the very low frequency limit, the phase velocities of the RCP and LCP waves (if ion motion is included) go to zero. This means that in order to get Alfven waves (see MHD waves) one has to use warm plasma theory, where the low frequency phase velocity is, approximately, Alfven velocity.

Propagation perpendicular to B (two wave modes)

ordinary waves
- identical to transverse waves in an isotropic plasma, i.e., the propagation is not affected by B
- propagating above the electron plasma frequency, w(pe)
- also here the reflection point frequency is affected by ions
- also called TEM (Transverse Electric-Magnetic) mode, since both the electric and magnetic fields are transverse to the direction of propagation (linear polarization)
extraordinary waves
- waves propagate in two frequency ranges: w(01)<w<w(UH) and w>w(02)
- also called TM (Transverse Magnetic) mode, since the magnetic fields are transverse to the direction of propagation
- electric field can have a longitudinal component (along k): these waves are thus partially longitudinal and partially transverse (elliptically polarized)
- if ion motion is taken into account, w<w(LH) branch is created; this branch relates to the low frequncy MHD (Alfven) waves.

Propagation at arbitrary directions

We are not going into details here (perhaps later)!

A phenomenon known as Faraday rotation occurs in the frequency range of RCP and LCP waves, and can be used as a plasma diagnostic tool.