(19) Motion in a Circle

In the absence of forces, motion in a straight line and constant velocity continues indefinitely. Motion in a circle, however, requires forces to act.

Imagine you have tied a stone to a string and are swinging it in a circle of some radius R (meters). Each rotation the stone covers a distance

2 p R meters

where p = 3.14159265359. . . is the ratio between the diameter of a circle and its circumference (to memorize, count digits in "Yes, I have a super motorbike to travel about the roads foolishly").

Imagine further that the stone makes N circuits ("revolutions") per second. Since its velocity v equals the distance it moves in one second, one finds

v = 2pNR m/sec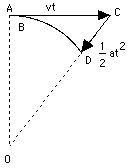

If the motion is followed just for a very brief moment, the path AB covered is so short that its curvature can be neglected, allowing one to view the motion as proceeding in a straight line, with velocity v. After a while, however, the difference between this motion and a straight-line one becomes obvious: the straight motion with velocity v would bring the particle to point C, at distance

AC = vt

while the actual motion brings it to some point D on the circle, whose center will be denoted by O.

It is useful to regard this motion as the sum of two separate motions: a straight-line motion from A to C, and then an added motion from C to D which returns the particle to the circle. As noted earlier (section on vectors), when a motion is the combination of two simpler motions, the resulting displacement can be obtained by deriving separately the displacements produced by each motion alone, then adding them together.

The added motion from C to D is the one of interest here. Its direction is always towards the center, and the distance CD covered by it--denoted here by x--can be obtained from the theorem of Pythagoras, applied to the triangle OAC (the calculation resembles the one which gave the distance to the horizon in section (8a)). In that triangle, OA = R, AC = vt, OC = R + x . Therefore

R² + v²t² = (R + x)² = R²+ 2Rx + x²

Subtract R² from both sides

v²t² = 2Rx + x² = x(2R + x)

If the time interval t is very short, x is much smaller than 2R and can be neglected by comparison. Then

v²t² = 2xR

or

x = 1/ 2 (v²/ R) t²

But by an earlier formula, in the section on acceleration, this is exactly the distance covered in time t by a motion with acceleration

a = v²/ R

The above result suggests that steady motion around a circle, at least for a short time span, can be viewed as the sum of a straight-line motion with fixed velocity v, plus an accelerated motion towards the center of attraction, with the above acceleration, a.

The conclusion is correct, even though the derivation is somewhat irregular. The conventional derivation (like most of the theory of motions) requires the use of differential calculus, the study of changing quantities and of the way they change, as well as familiarity with vectors.