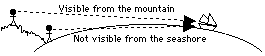(8) The Round Earth and Christopher Columbus
The method of labeling points on the surface of the Earth resembles the one used on the celestial sphere, except that where one measures "declination" and "right ascension" on the celestial sphere, those angles are called "latitude" and "longitude" on the globe of the Earth. "Zero longitude," from which all other values are measured, is the longitude of the Royal Astronomical Observatory in Greenwich, at the eastern edge of London, England. The observatory is now a museum and visitors there are shown a brass ribbon stretching across the yard, marking the line of zero longitude ("zero meridian"). Today it is well known that the Earth is a sphere, or very close to one (its equator bulges out a bit because of the Earth's rotation). When Christopher Columbus proposed to reach India by sailing west from Spain, he too knew that the Earth was round. India was the source of precious spices and other rare goods, but reaching it by sailing east was difficult, because Africa blocked the way. On a round globe, however, it should also be possible to reach India by sailing west, and this Columbus proposed to do (he wasn't the first one to suggest this--see below). Sometimes the claim is made that those who opposed Columbus thought the Earth was flat, but that wasn't the case at all. Even in ancient times sailors knew that the Earth was round and scientists not only suspected it was a sphere, but even estimated its size. If you stand on the seashore and watch a ship sailing away, it will gradually disappear from view. But the reason cannot be the distance: if a hill or tower are nearby, and you climb to the top after the ship has completely disappeared, it becomes visible again. Furthermore, if on the shore you watch carefully the way the ship disappears from view, you will notice that the hull vanishes first, while the masts and sails (or the bridge and smokestack) disappear last. It is as if the ship was dropping behind a hill, which in a way is exactly the case, the "hill" being the curve of the Earth's surface. Erathosthenes, Posidonius and El MamunThe Greek philosopher Erathosthenes went one step further and actually estimated how large the Earth was. He was told that on midsummer day (June 21) in the town of Syene in southern Egypt (today Aswan, near a huge dam on the river Nile) the noontime Sun was reflected in a deep well, meaning that it was right overhead, at zenith. Erathosthenes himself lived in Alexandria, near the river's mouth, north of Syene, about 5000 stadia north of Syene (the stadium, the size of a sports arena, was a unit of distance used by the Greeks). In Alexandria the Sun on the corresponding date did not quite reach zenith, and vertical objects still threw a short shadow. Erathosthenes established that the direction of the noon Sun differed from the zenith by an angle that was 1/50 of the circle, that is, 7. 2 degrees, and from that he estimated the circumference of the Earth to be 250,000 stadia. Other estimates of the size of the Earth followed. Some writers reported that the Greek Posidonius used the greatest height of the bright star Canopus above the horizon, as seen from Egypt and from the island of Rhodes further north (near the southwestern tip of Turkey). He obtained a similar value, a bit smaller. The Arab Khalif El Ma'mun, who ruled in Baghdad from 813 to 833, sent out two teams of surveyors to measure a north-south baseline and from it also obtained the radius of the Earth. Compared to the value known today, those estimates were pretty close to the mark. The idea of sailing westward to India dates back to the early Romans. According to Dr. Irene Fischer, who studied this subject, the Roman writer Strabo, not long after Erathosthenes and Posidonius, reported their results and noted: "if of the more recent measurements of the Earth, the one which makes the Earth smallest in circumference be introduced--I mean that of Posidonius who estimates its circumference at about 180,000 stadia, then. . . " and he continues: "Posidonius suspects that the length of the inhabited world, about 70,000 stadia, is half the entire circle on which it had been taken, so that if you sail from the west in a straight course, you will reach India within 70,000 stadia. " Notice that Strabo--for unclear reasons--reduced the 250,000 Stadia of Erathosthenes to 180,000, and then stated that half of that distance came to just 70,000 stadia. Handling his numbers in that loose fashion, he could argue that India was not far to the west. Columbus AgainAll these results were known to the panel of experts which King Ferdinand appointed to examine the proposal made by Columbus. They turned Columbus down, because using the original value by Erathosthenes, they calculated how far India was to the west of Spain, and concluded that the distance was far too great.
Columbus had an estimate of his own. Some historians have proposed that he used an argument like Strabo's, but Dr. Fischer found his claim to be based on incorrect units of distance. Columbus used an erroneous estimate by Ptolemy (whom we meet again), who based it on a later definition of the stadium, and in estimating the size of the settled world he confused the Arab mile, used by El Ma'mun, with the Roman mile on which our own mile is based. All the same, his final estimate of the distance to India was close to Strabo's. In the end Queen Isabella overruled the experts, and the rest is history. We may never know whether Columbus knowingly fudged his values to justify an expedition to explore the unknown, or actually believed India was not too far to the west of Spain. He certainly did call the inhabitants of the lands he discovered "Indians," a mislabeling which still persists. But we do know that if the American continent had not existed, the experts would have been vindicated: Coumbus with his tiny ships could never have crossed an ocean as wide as the Atlantic and Pacific combined. In hindsight the exploration of the unknown may be justification enough! As for the size of the Earth, it was accurately measured many times since (see item "geodesy" in an encyclopaedia), one notable effort being that of the French Academy of Sciences in the late 1700s. Their aim was to devise a new unit of distance, equal to one part in 10,000,000 of the distance from the pole to the equator (as Erathostenes showed, it is enough to measure part of that distance). Nowadays that distance is known even more accurately, but the unit introduced by the French academy is still used as the standard of all distance measurements. It is called the meter. |