Надежность. Существуют два различных способа использования этого термина:
Надежность и позиционный анализ. В этом контексте понятие надежности определяется, как степень точности измерения истинных значений (например, индивидуальных предпочтений) с помощью многомерной шкалы относительно ошибки измерения. Похожее понятие надежности шкалы иногда используется при оценивании надежности процесса или шкал измерения в картах контроля качества. За дополнительной информацией обратитесь к разделу Надежность и позиционный анализ или к описанию повторяемости и воспроизводимости в главе Анализ процессов.
Анализ Вейбулла и анализ
надежности/времени отказов. В этом
контексте понятие надежности определяется,
как функция вероятности отказа тестируемой
единицы (или смерти субъекта) в зависимости от
времени. Формально функция надежности (обычно
обозначаемая через R(t)) является дополнением
функции распределения до 1 (т.е. R(t)=1-F(t));
функция надежности также иногда называется
функцией выживания (равна вероятности дожития до
момента t; см. например Lee, 1992). За дополнительной
информацией обратитесь к разделу Анализ надежности/времени
ошибки в главе Анализ
процессов.
Надежность
и позиционный анализ. Во многих областях
исследований (особенно связанных с измерением
личностных характеристик) точные измерения сами
по себе представляют сложную задачу. Например, в
психологии точное измерение личностных
характеристик или отношений к чему-либо -
необходимый первый шаг, предваряющий всякую
теорию. В целом, очевидно, что во всех социальных
дисциплинах ненадежные измерения препятствуют
попытке предсказать поведение людей. В
прикладных исследованиях, когда наблюдения над
переменными затруднены, также важна точность
измерений. Например, надежное измерение
производительности служащих, как правило,
является сложной задачей. Однако очевидно, что
эти измерения необходимы для любой системы
оплаты, основанной на производительности труда.
Методы анализа надежности и позиционного анализа позволяют как построить надежные шкалы, так и улучшить надежность уже используемых шкал. Эти методы помогают при конструировании и оценивании суммарных шкал, т.е. шкал, которые используются при многократных измерениях. Программа вычисляет многочисленные статистики, позволяющие оценить надежность шкалы с помощью классической теории тестирования.
За дополнительной информацией обратитесь к разделу Надежность и позиционный анализ.
Понятие надежности определяется также и
как функция вероятности отказа (смерти) в
зависимости от времени. Для обсуждения понятия
надежности в применении к контролю качества
(например, в промышленной статистике) обратитесь
к разделу Анализ
надежности/времени ошибки в главе Анализ
процессов (см. там же раздел Повторяемость и
воспроизводимость). Для сравнения этих (очень
разных) понятий см. раздел Надежность.
Наименьшие
квадраты (подгонка на 2М графиках). В
соответствии с процедурой сглаживания методом
взвешенных относительно расстояния наименьших
квадратов кривая подгоняется к координатам XY
данных таким образом, что влияние отдельных
точек уменьшается с увеличением расстояния по
горизонтали от соответствующих точек на кривой.
Наименьшие
квадраты (подгонка на 3М графиках). В
соответствии с процедурой сглаживания методом
взвешенных относительно расстояния наименьших
квадратов поверхность подгоняется к координатам
XYZ таким образом, что влияние отдельных
точек уменьшается с увеличением расстояния по
горизонтали от соответствующих точек на
поверхности.
Невзвешенные
средние. Если при проведении
многофакторного дисперсионного
анализа частоты в ячейках не совпадают,
программа вычисляет невзвешенные средние (на
уровнях фактора) на основании средних по
подгруппам без использования весов, т.е. без
учета различий в частотах по подгруппам.
Независимые
и зависимые переменные. Термины зависимая
и независимая переменная обычно
применяются в экспериментальных исследованиях,
где приходится манипулировать некоторыми
переменными. В этом смысле "независимость"
переменной определяется как независимость от
реакции, свойств и намерений объектов
эксперимента и т.п. Некоторые переменные
предполагаются "зависимыми" от действий
объекта эксперимента или условий эксперимента.
Эти переменные, возможно в неявной форме,
содержат некоторую информацию о поведении или
реакции объекта в ходе эксперимента. Независимые
переменные - это переменные, значениями которых
можно управлять, а зависимые переменные - это
переменные, которые можно только измерять или
регистрировать.
Некий противоположный смысл эти термины получают в случае проведения исследований, в которых мы не можем прямо изменять независимые переменные, а можем только отнести объекты к некоторой "экспериментальной группе" на основании некоторых существующих заранее свойств объектов. Например, если в эксперименте сравнивается число лейкоцитов (WCC) в крови мужчин и женщин, то Пол можно назвать независимой переменной, а WCC - зависимой переменной.
Подробнее см. раздел Зависимые и независимые переменные.
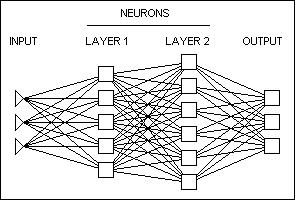
Нейрон. Элемент нейронной сети.
Нейронные сети.
Класс аналитических методов, построенных на
(гипотетических) принципах обучения мыслящих
существ и функционирования мозга и позволяющих
прогнозировать значения некоторых переменных в
новых наблюдениях по данным других наблюдений
(для этих же или других переменных) после
прохождения этапа так называемого обучения на
имеющихся данных.

Дополнительную информацию см. в разделах Добыча данных и Нейронные сети STATISTICA.
Нелинейное
оценивание. Иногда, при проведении анализа
линейной модели, исследователь получает данные о
том, что модель неадекватна. В этом случае его
по-прежнему интересует зависимость между
предикторными переменными (независимыми) и
откликом (зависимой),
но для уточнения модели в уравнение добавляются
некоторые нелинейные члены. Например, его
можно использовать для уточнения зависимости
между дозой и эффективностью лекарства, стажем,
работы и производительностью труда, стоимостью
дома и временем, необходимым для его продажи и
т.д. Наверное, вы заметили, что ситуации,
рассматриваемые в этих примерах, часто
интересовали нас и в таких методах как
множественная регрессия (см. Множественная
регрессия) и дисперсионный анализ (см. Дисперсионный анализ). На
самом деле, нелинейное
оценивание можно считать обобщением
этих двух методов. Так, в методе множественной
регрессии (и в дисперсионном анализе ANOVA)
предполагается, что зависимость отклика от предикторных
переменных линейна. В нелинейном оценивании
выбор характера зависимости остается за вами.
Например, вы можете определить зависимую
переменную как логарифмическую функцию от предикторной
переменной, как степенную функцию или как любую
другую композицию элементарных функций от
предикторов. (Однако если все изучаемые
переменные имеют категориальную природу, или
могут быть преобразованы к категориальным
переменным, в качестве альернативы нелинейной
регрессии можно использовать анализ
соответствий.)
Подробнее см. раздел Нелинейное
оценивание.
Непараметрическая
статистика. Непараметрические методы
используются в случае, когда неизвестны
параметры распределения исследуемой выборки
(отсюда и термин "непараметрическая
статистика") или переменные измеренные в
бедной шкале (например, в номинальной или
порядковой). Также их применяют, если объемы
данных недостаточны для применения
параметрических методов (например, основанных на
предположении нормальности исходных данных).
Непараметрические методы не основываются на
оценках параметров распределения (такие как,
например, среднее или стандартное отклонение),
описывающих распределение интересующей выборки.
Эти методы иногда называются свободными от
параметров или свободными от распределения.
За дополнительной информацией обратитесь к
разделу Непараметрическая
статистика в главе Элементарные
понятия статистики.
Несимметричное
распределение. Если вы разобьете такое
распределение пополам в точке среднего (или
медианы), то распределения значений с двух сторон
от этой центральной точки будут неодинаковыми
(т.е. несимметричными). Такое распределение можно
назвать "скошенным".
См. также Описательные
статистики - Введение.
Нет
сезонности, демпфированный тренд. В этой
модели анализа временных
рядов прогнозы простого экспоненциального
сглаживания "улучшаются" демпфированным
трендом [сглаживается независимо с параметром ![]() для тренда и параметром
для тренда и параметром
![]() для эффекта
затухания]. Например, пусть вы прогнозируете
процент семей, имеющих определенное электронное
устройство (например, видеомагнитофон). Каждый
год доля семей, имеющих собственный
видеомагнитофон, увеличивается, однако это
увеличение демпфировано, иными словами
возрастание тренда постепенно уменьшается, так
как с течением времени рынок насыщается.
для эффекта
затухания]. Например, пусть вы прогнозируете
процент семей, имеющих определенное электронное
устройство (например, видеомагнитофон). Каждый
год доля семей, имеющих собственный
видеомагнитофон, увеличивается, однако это
увеличение демпфировано, иными словами
возрастание тренда постепенно уменьшается, так
как с течением времени рынок насыщается.
Прежде всего, необходимо вычислить начальные значения S0 и T0. Эти значения вычисляются по формуле:
T0 = (1/![]() )*(Xn-X1)/(N-1)
)*(Xn-X1)/(N-1)
где
N - число наблюдений в ряде
![]() -параметр сглаживания для
демпфированного трендa
-параметр сглаживания для
демпфированного трендa
и S0 = X1-T0/2
Нет
сезонности, линейный тренд.
(двухпараметрический метод Холта)
В этой модели анализа временных
рядов в прогнозе учитывается линейный
тренд в данных, который сглаживается независимо
с помощью параметра ![]() (гамма) (см. также оценивание
параметров тренда). Этот метод называется
также двухпараметрическим методом Холта.
Эта модель, например, адекватна для прогноза
запасных частей. Потребность запасных частей для
машинного парка может медленно увеличиваться
или уменьшаться с течением времени (трендовая
компонента), тренд может медленно изменяться
из-за старения машин и других факторов.
(гамма) (см. также оценивание
параметров тренда). Этот метод называется
также двухпараметрическим методом Холта.
Эта модель, например, адекватна для прогноза
запасных частей. Потребность запасных частей для
машинного парка может медленно увеличиваться
или уменьшаться с течением времени (трендовая
компонента), тренд может медленно изменяться
из-за старения машин и других факторов.
Прежде всего необходимо вычислить начальные значения S0 и T0. Эти значения вычисляются по формуле:
T0 = (Xn-X1)/(N-1)
где
N - длина ряда
и S0 = X1-T0/2
Нет сезонности,
с исключенным трендом. Эта модель в анализе
временных рядов
эквивалентна модели простого экспоненциального
сглаживания. Заметим, что по умолчанию
начальное значение S0 будет вычислено,
как среднее всех наблюдений.
Нет
сезонности, экспоненциальный тренд. В этой
модели анализа временных
рядов прогноз простого экспоненциального
сглаживания "улучшается" с помощью
экспоненциального тренда [сглаженного с
параметром ![]() (гамма)].
Например, пусть вы хотите предсказать общие
месячные затраты на ремонт производственного
оборудования. Возможно, в затратах имеется
экспоненциальный тренд, означающий, что из года в
год затраты увеличиваются на определенный
процент или в определенное число раз. Как
результат, имеем постепенное экспоненциальное
возрастание абсолютных долларовых затрат на
ремонт.
(гамма)].
Например, пусть вы хотите предсказать общие
месячные затраты на ремонт производственного
оборудования. Возможно, в затратах имеется
экспоненциальный тренд, означающий, что из года в
год затраты увеличиваются на определенный
процент или в определенное число раз. Как
результат, имеем постепенное экспоненциальное
возрастание абсолютных долларовых затрат на
ремонт.
Для вычисления сглаженных значений в первом сезоне необходимы начальные значения сезонных компонент. По умолчанию S0 и T0 (начальный тренд) вычисляются по формуле:
T0 = (X2/X1)
и
S0 = X1/T01/2
Неуправляемое
обучение (для нейронных сетей). Алгоритмы
обучения, в которых на вход нейронной
сети подаются данные, содержащие только
значения входных переменных. Такие алгоритмы
предназначены для нахождения кластеров во
входных данных.
См. также алгоритм
Кохонена.
Номинальная шкала.
Это категориальная (т.е. качественная, а не
количественная) шкала измерения, где каждое
значение определяет отдельную категорию, в
которую попадают значения переменной (каждая
категория "отличается" от других, но это
отличие не может быть количественно измерено).
См. также раздел Элементарные
понятия статистики.
Номинальные
переменные. Переменные, которые могут
принимать конечное множество значений, например,
Пол = {Муж, Жен}. В нейронных
сетях номинальные выходные переменные
используются в задачах классификации,
в отличие от задач регрессии.
См. также Группирующие (или
кодирующие) переменные и Шкала
измерений.
Нормальная подгонка.
Нормальные/наблюдаемые гистограммы являются
наиболее распространенным графическим способом
проверки нормальности. При выборе этой подгонки
на распределение частот будет наложена
нормальная кривая. Нормальная функция подгонки к
гистограмме определяется так:
f(x) = NC * step * normal(x, среднее, ст.откл.)
Нормальная функция подгонки к гистограмме с накопленными частотами определяется так:
f(x) = NC * inormal(x, среднее, ст.откл.)
где
NC - число наблюдений.
step - размер шага
категоризации (например, 1).
normal - нормальная функция
inormal - интеграл
нормальной функции.
См. также разделы Нормальное
распределение и Двумерное нормальное
распределение.
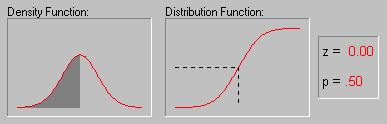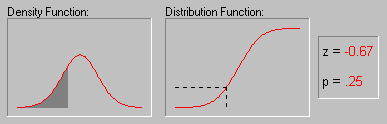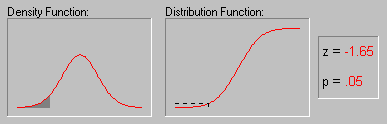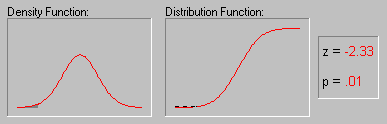
Нормальное
распределение. Нормальное распределение
(этот термин был впервые использован Гальтоном в
1889 г.), также иногда называемое гауссовским,
определяется следующим образом:
f(x) = 1/[2*![]() )1/2*
)1/2*![]() ] * e**{-1/2*[(x-µ)/
] * e**{-1/2*[(x-µ)/![]() ]2}
]2}
-![]() < x <
< x < ![]()
где
µ - среднее
![]() - стандартное
отклонение
- стандартное
отклонение
e - число Эйлера (2.71...)
![]() - число Пи (3.14...)
- число Пи (3.14...)
См. также разделы Двумерное
нормальное распределение, Элементарные
понятия статистики (нормальное распределение),
Основные статистики - Критерии
нормальности.
Нормальные
вероятностные графики. Этот график
используется для оценки нормальности
распределения переменной, т.е. близости этого
распределения к нормальному. Зависимость между
выбранной переменной и "ожидаемыми от
нормального распределения" значениями
изображается на диаграмме рассеяния.
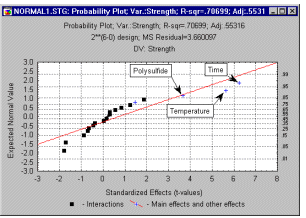
Стандартный нормальный вероятностный график строится следующим образом. Сначала все значения упорядочиваются по рангу. По этим рангам рассчитываются значения z (т.е. стандартизованные значения нормального распределения) в предположении, что данные имеют нормальное распределение (см. вычислительные замечания). Эти значения z откладываются по оси Y графика. Если наблюдаемые значения (откладываемые по оси X) распределены нормально, то все значения на графике должны попасть на прямую линию. Если значения не являются нормально распределенными, они будут отклоняться от линии. На этом графике можно легко обнаружить выбросы. Если наблюдается очевидное несовпадение, а данные располагаются относительно линии определенным образом (например, в виде буквы S), то к ним, вероятно, можно применить какое-либо преобразование.
См. также раздел Нормальные
вероятностные графики (вычислительные
замечания)
Нормальные вероятностные графики (вычислительные замечания). Для вычисления по рангам ожидаемых нормальных вероятностных значений, т.е. соответствующих нормальных z-значений, используются следующие формулы.
Нормальный вероятностный график. Нормальное вероятностное значение zj для j-го значения (ранга) переменной с N наблюдениями вычисляется так:
z j = ![]() -1 [(3*j-1)/(3*N+1)]
-1 [(3*j-1)/(3*N+1)]
где where ![]() -1
есть обратная функция нормального распределения
(превращающая нормальную вероятность p в
нормальное значение z).
-1
есть обратная функция нормального распределения
(превращающая нормальную вероятность p в
нормальное значение z).
Полунормальный вероятностный график. В этом случае полунормальное вероятностное значение zj для j-го значения (ранга) переменной с N наблюдениями вычисляется так:
z j = ![]() -1 [3*N+3*j-1)/(6*N+1)]
-1 [3*N+3*j-1)/(6*N+1)]
где where ![]() -1
есть обратная функция нормального
распределения.
-1
есть обратная функция нормального
распределения.
Нормальный вероятностный график с исключенным трендом. На этом графике каждое значение (xj) стандартизируется путем вычитания среднего и деления на соответствующее стандартное отклонение (s). Нормальное вероятностное значение с исключенным трендом zj для j-го значения (ранга) переменной с N наблюдениями вычисляется так:
z j = ![]() -1 [(3*j-1)/(3*N+1)] - (x j-среднее)/s
-1 [(3*j-1)/(3*N+1)] - (x j-среднее)/s
где ![]() -1
есть обратная функция нормального
распределения.
-1
есть обратная функция нормального
распределения.
Нормальные
вероятностные графики с исключенным трендом.
Этот график используется для оценки
нормальности распределения переменной, т.е.
близости этого распределения к нормальному.
Зависимость между выбранной переменной и
"ожидаемыми от нормального распределения"
значениями изображается на диаграмме рассеяния.
Этот график строится тем же способом, что и стандартный нормальный
вероятностный график, с тем отличием, что перед
построением графика удаляется линейный тренд.
При этом часто получается более
"развернутая" картина, позволяющая
пользователю легче обнаружить закономерности
отклонений.
Нормировка.
Корректировка длины вектора посредством
некоторой суммирующей функции (например, на
единичную длину или на единичную сумму
компонент).